
いつまでも終わりのない円周率。
π(パイ)や3.14と言う事は知っていても、その本当の意味を知らない人も多いのかと思います。
もちろん、義務教育で勉強してきた事なので知っていないとダメなのですが、忘れてしまっている事もあるでしょう。
そこで、今回は円周率とは、そもそも何なのかを徹底解説していきます。
円周率ってそもそも何なの?
円周率とは、円の周長の直径に対する比率です。
もう少し簡単に言うと、直径を1とした時、円の周りの長さが約3.14倍となり、その数字を円周率と呼んでいます。
そして、約3.14では面倒なのでπ(パイ)と呼ばれる記号に置き換えて使っているのです。
画像で説明すると、こんな感じです。
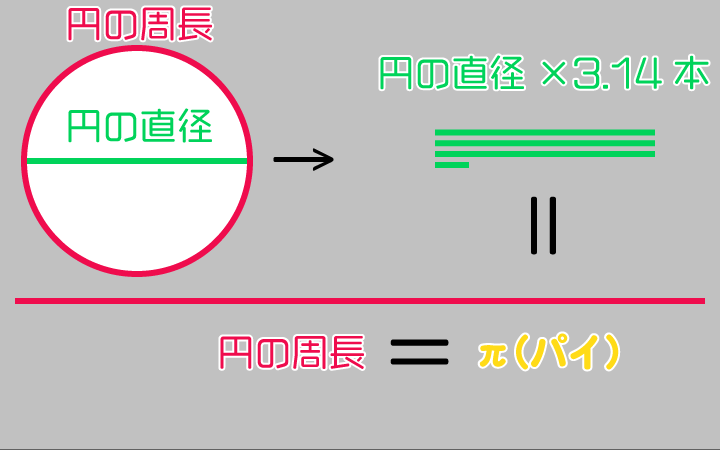
おそらく、9割の人は理解している事だと思いますが、こう見ると円周率と言うのは、とてもシンプルに見えます。
円周率はなぜ無限に続くのか?
上の図を見て頂いた通り、円周の長さを測る事が出来れば、円周率に終わりが存在すると言えます。
どういうことかと言うと、直径1センチの円を用意します。
その円の周りの長さを正確に測定する事が出来れば、円周率に終わりは来るのです。
図でいうと、下にある「赤い線」の長さを正確に測る事が出来れば、円周率の謎は解決します。
こう考えると、現実世界に存在させる事が出来るのに、終わりが無いのはおかしいと思いませんか?
測定器で測ってしまえば、一瞬で分かりそうです。
しかし、現実世界に存在する物でも正確な数字を出せない事例は他にもあります。
例えば、下の箱を正確な3等分になるように、縦線を2本追加してください。
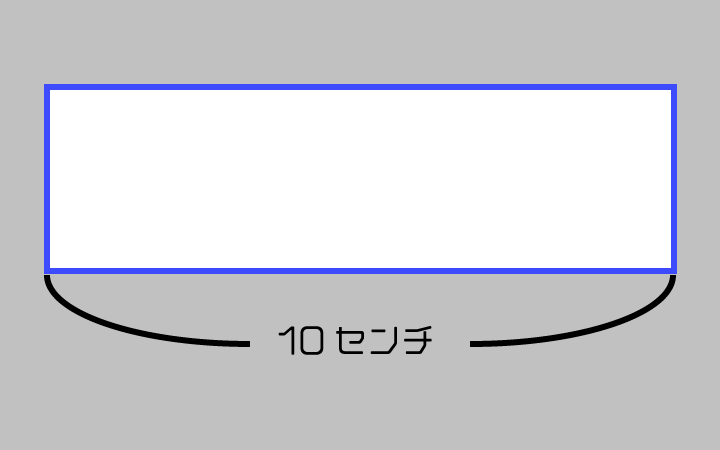
見た目は、3等分出来るかもしれませんが、正確な3等分にしようとすると、3.333333…cmとなってしまい、いつまで経っても3等分出来る事はありません。
これは、どこまでも正確に測れる測定器があったとしても同じです。
このように、現実世界に存在させることが出来る物でも正確な数字を出せない事はあるのです。
もっと分かりやすく解説
10cmの箱を3等分に出来ないのは理解をしてもらえたと思いますが、「存在する物の長さが測れない」は理解できないという人も多いと思います。
しかし、これに関しては数学の難しい方式を使って円周率に終わりがない事を証明してしまっているのですから仕方がありません。
この証明を誰にでもわかるように解説しようとすると、別の公式など数学全体を理解しないといけないので、一から授業をする必要があります。
ただ、この状態を簡単に説明する方法も存在します。
それが次のような状態です。

ここまでは、先ほど円周率の意味を説明した時の作業と同じですね。
そしてこれを測っていきます。
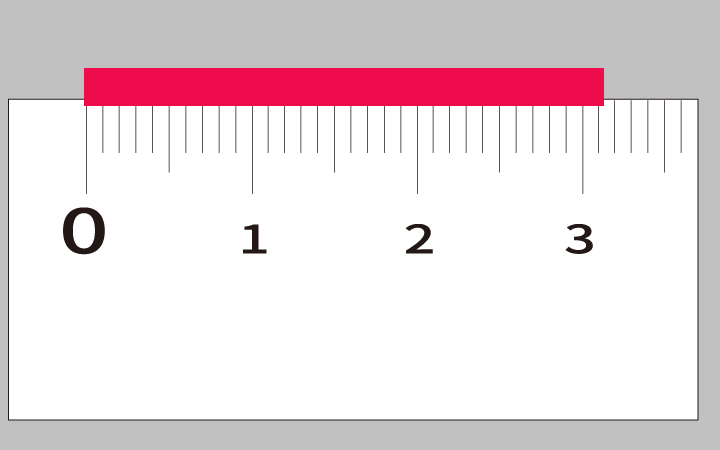
よく見ていただいたら分かる通り、目盛りと目盛りの間です。
なので、もっと細かい定規を用意してみましょう。

またもや、目盛りと目盛りの間でしたね。
もっともっと、細かい定規を用意してみましょう。
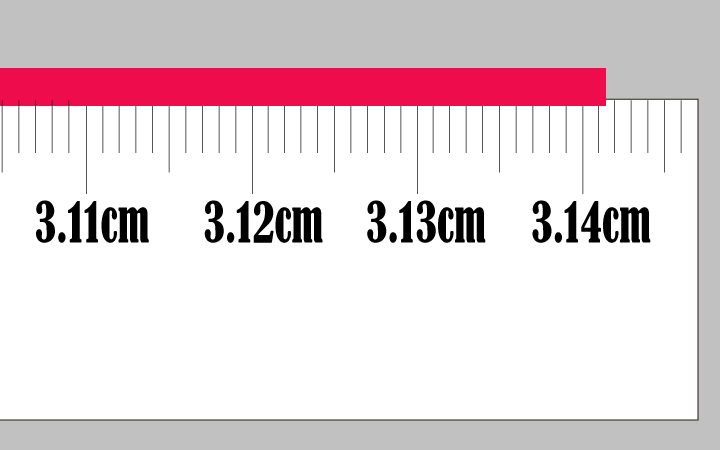
またまた、目盛りと目盛りの間でした。
そして、この作業を22兆4591億5771万8361回繰り返しても、同じようになってしまいます。(2016年現在)
つまり、人類は円周の正確な長さを測る事は出来ていないと言う事です。
そして、この作業は無限に続くと言う事が証明されています。
もちろん、人間が証明した事に過ぎませんので、もしかすると世紀の大発見が起こるかもしれません。
少なくとも、現時点では数学的証明がされた事で覆った事は聞いたことはありませんが・・・。
これが、円周率の正体です。
日常生活で使う事は少ないですが、覚えておけば何かの役に立つことがあるかも?しれませんね。

≪…人類は円周の正確な長さを測る事は出来ていないと言う事…≫こそ、数学の基となる自然数が大和言葉の【 ひ・ふ・み・よ・い・む・な・や・こ・と 】からの送りモノとして眺めると、[数のヴィジョン]になるとか・・・
自然数のキュレーション的な催しがあるといいなぁ~
≪…人類は円周の正確な長さを測る事は出来ていないと言う事…≫について、
こんな記事を見つけ、
【 半径(はんけい)r の円の面積(めんせき)と1辺(ぺん)がr の正方形の面積(めんせき)の比(ひ)でもある。】
から、
1辺(1)の正方形で、半径(1)の円をなぞり逢きった時の比と捉えたい。
数学の基となる自然数の[1]を数の言葉ヒフミヨ(1234)が、平面(2次元)からの送りモノとして眺めると、
数の言葉(ひ・ふ・み・よ・い・む・な・や・こ・と)
言葉の点線面
カタチ(〇△□ながしかく)
演算符号(+-×÷√=)
十進法の基における西洋数学の成果の符号(i e π)
無限(∞) [1] [0]
数式 方程式
直交座標 極座標
自然数[1]の存在量化(∃)
数字(2 3 4 5 6 7 8 9)
などをウマクウマク纏め上げている。
1・2・3・4次元で閉じ(計算でき)ているのを、自然(じねん)に辿り着く風景は、絵本の力で・・・
哲学してみる
こんとん
みどりのトカゲとあかいながしかく
サンカクさん
シカクさん
まんまるさん
あかちゃんのわらべうた
さよならさんかくまたきてしかく
すうがくでせかいをみるの
もろはのつるぎ
終活の△仏魂棚に (母の日に臍をみつめてヒフミヨに)
πっていうやつを使わない、簡単な説明ってできますか?
まだ習ってないんです…(泣)
≪…πっていうやつを使わない、簡単な説明ってできますか?…≫を、立体の円すい・球・円柱に観る。数の言葉ヒフミヨ(1234)が、カタチからの送りモノとして眺めると、平面(2次元)からの影(投影)の送りモノとして眺められ円(π)が仲立ちして、自然数の1 2 3 を味える。
上下(重力方向)が、円の影で[π]を隠し、左右(水平方向)で、△ 〇 ▢ と観える。
このコトの光景は、「ちしきのもり 日本の算数 和算って、なあに?」小寺裕著の【底面と高さが等しい円柱と円すいそしてこの円柱にぴったり入る球があるとき、これらの円すい、球、円柱の体積比は1:2:3となる。】とある。
ヒフミヨは1とπとのお友達
1 2 3 4 の関係は、2冊の絵本の力で・・・
すうがくでせかいをみるの
もろはのつるぎ(『自然比矩形』)